Clémence Magnien, Matthieu Latapy and Michel Habib
ACM Journal of Experimental Algorithmics (JEA), 13, 2009
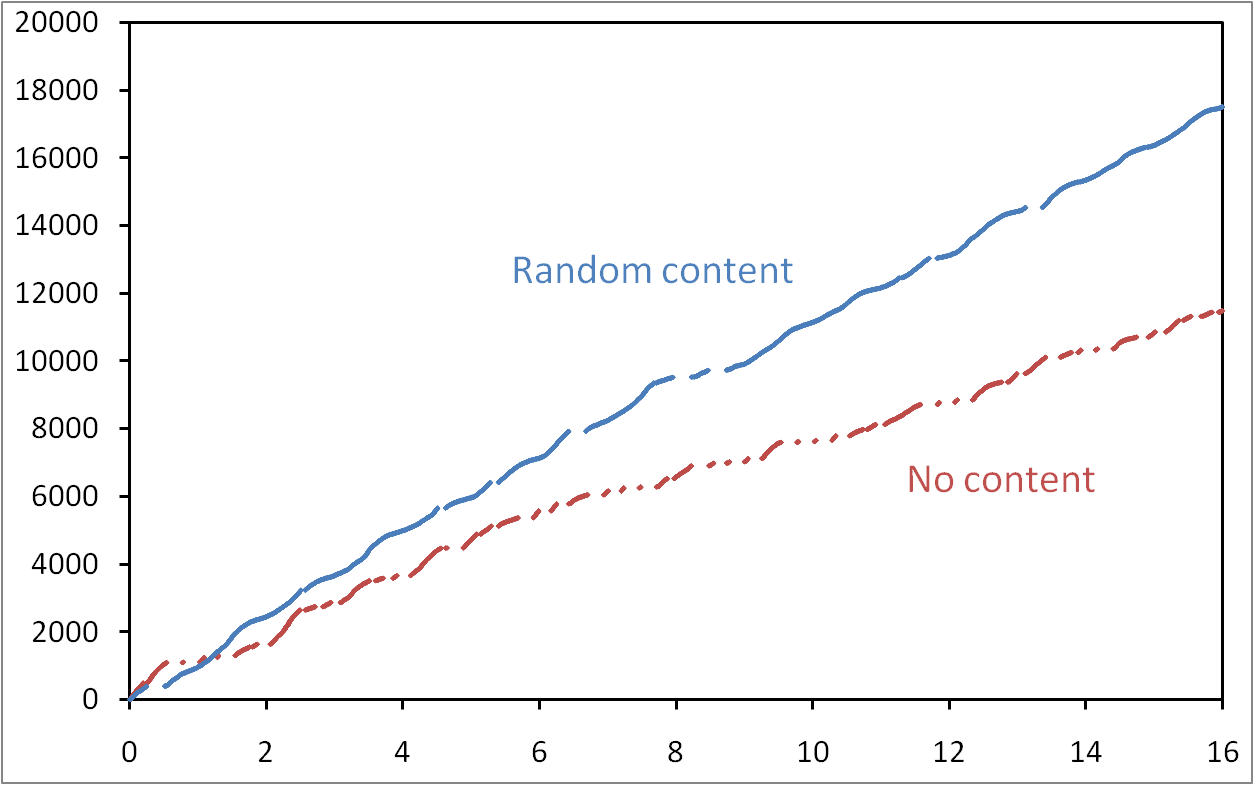
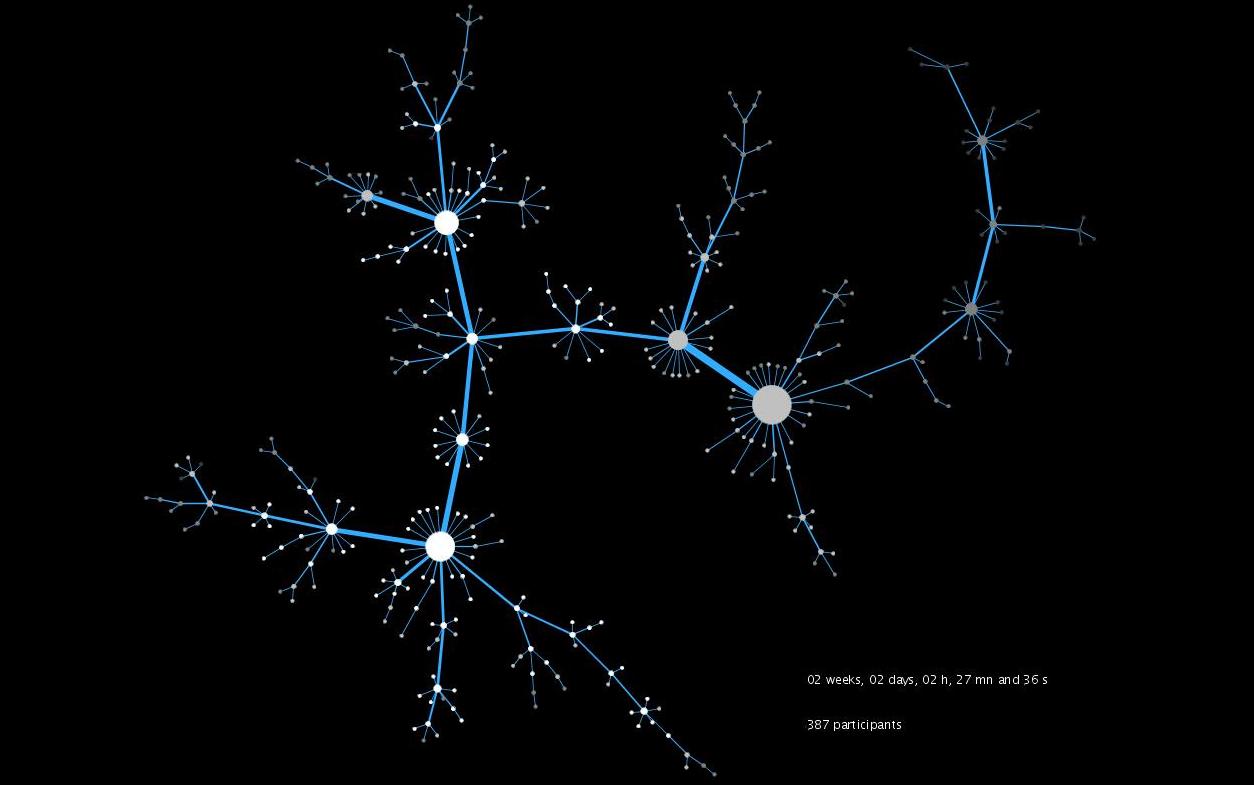
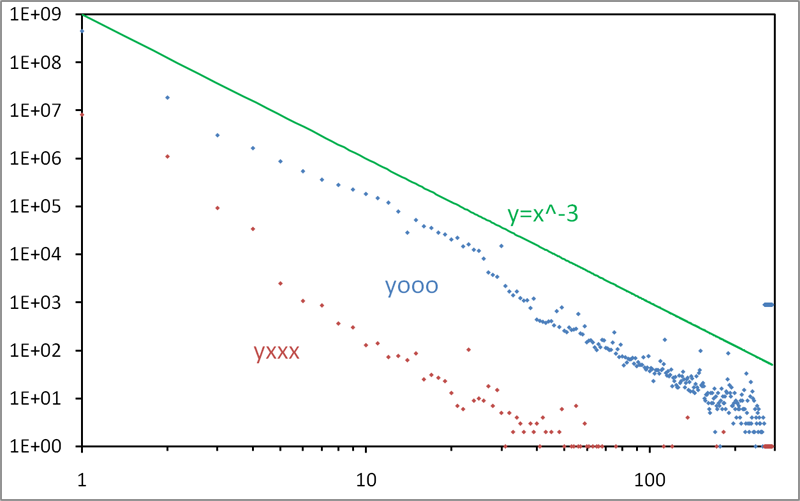
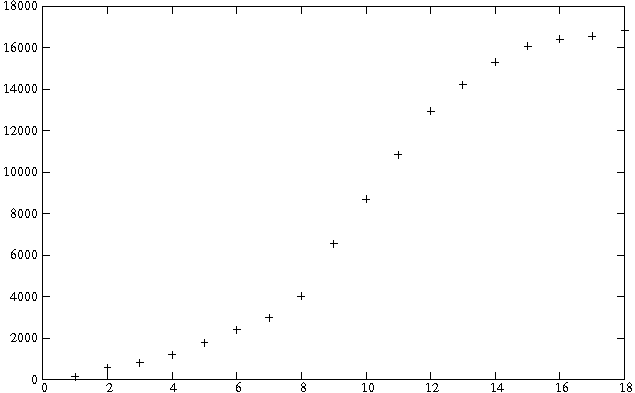
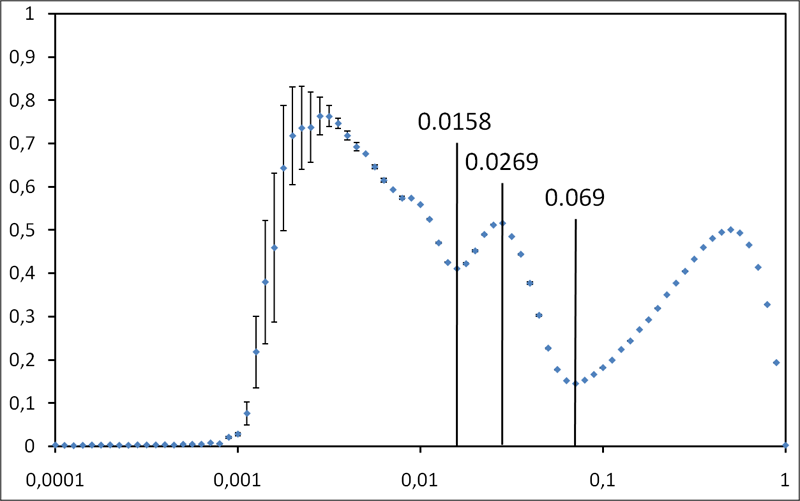
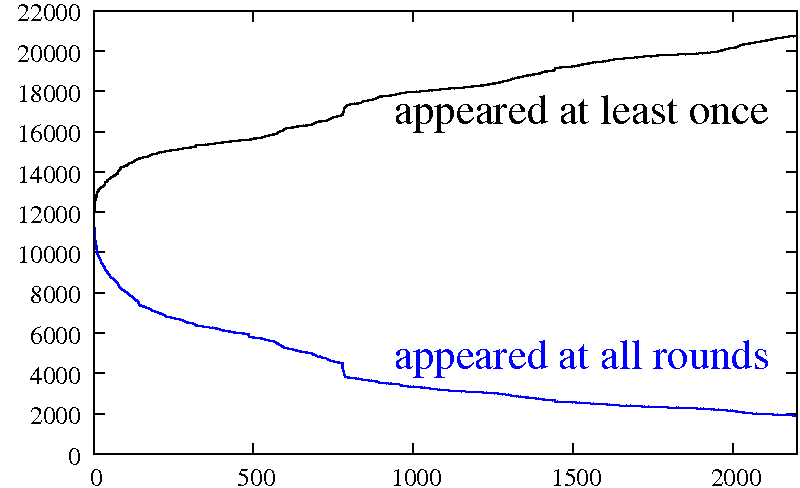
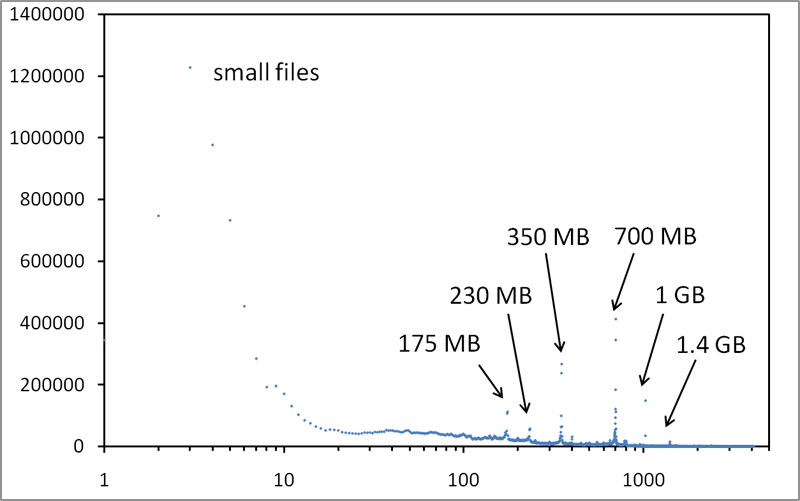
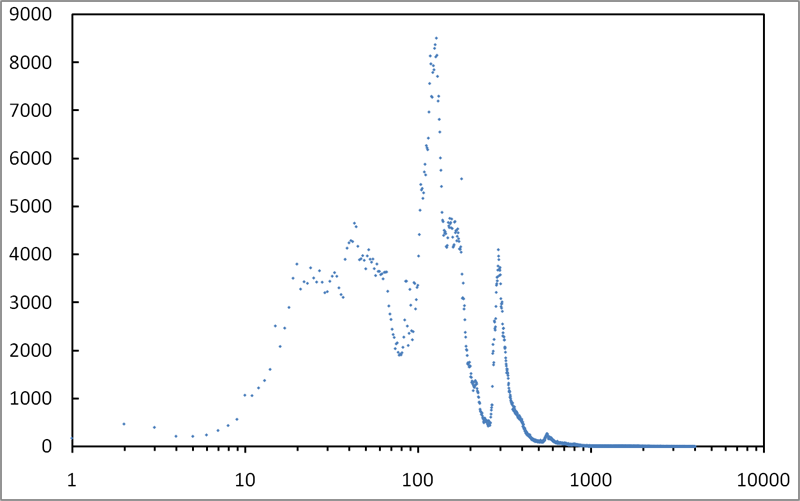
The diameter of a graph is among its most basic parameters. Since a few years, it moreover became a key issue to compute it for massive graphs in the context of complex network analysis. However, known algorithms, including the ones producing approximate values, have too high a time and/or space complexity to be used in such cases. We propose here a new approach relying on very simple and fast algorithms that compute (upper and lower) bounds for the diameter. We show empirically that, on various real-world cases representative of complex networks studied in the literature, the obtained bounds are very tight (and even equal in some cases). This leads to rigorous and very accurate estimations of the actual diameter in cases which were previously untractable in practice.