Impact of Random Failures and Attacks on Poisson and Power-Law Random Networks
Clémence Magnien, Matthieu Latapy and Jean-Loup Guillaume
ACM Computing Surveys, 43 (3), 2011. Extended abstract published in LNCS, proceedings of the 8-th International Conference On Principles Of Distributed Systems OPODIS’04, 2004, Grenoble, France (title: Comparison of Failures and Attacks on Random and Scale-free Networks)
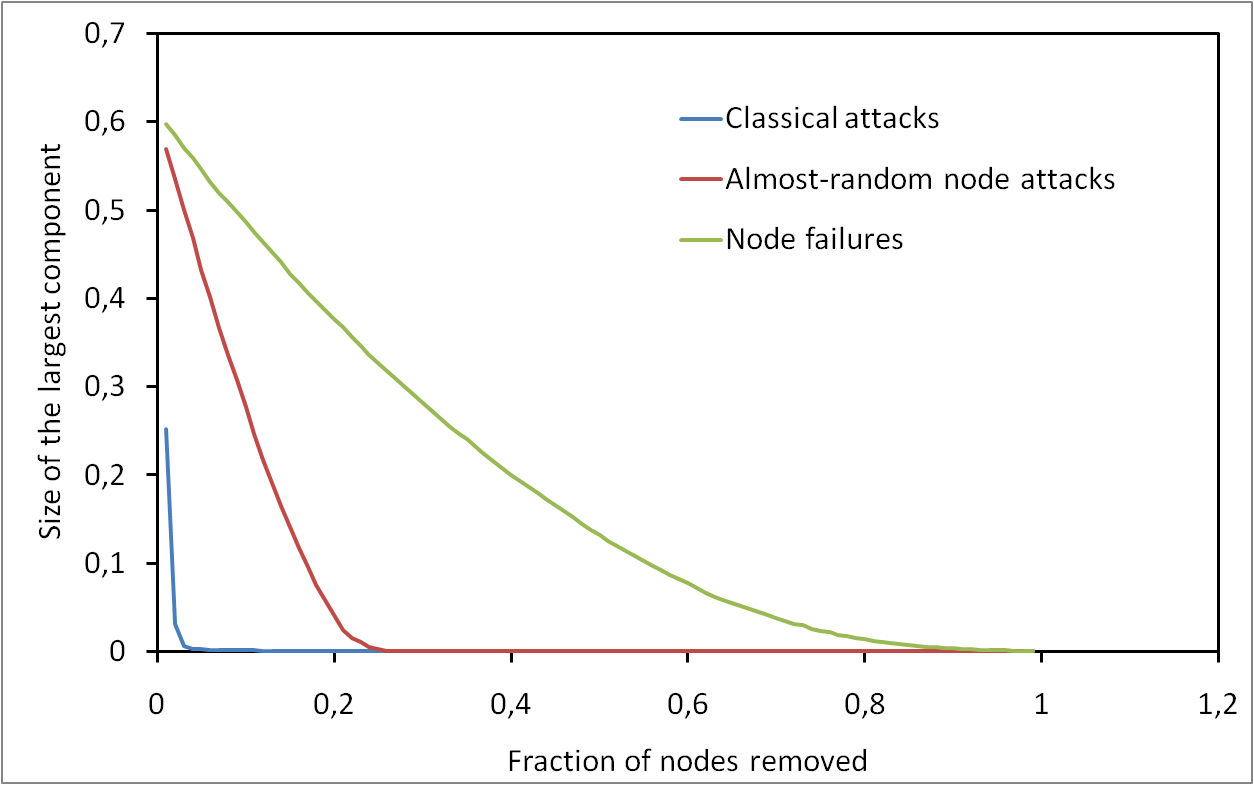
It appeared recently that the underlying degree distribution of a network may play a crucial role concerning its robustness. Empiric and analytic results have been obtained, based on asymptotic and mean-field approximations. Previous work insisted on the fact that power-law degree distributions induce a high resilience to random failure but a high sensitivity to some attack strategies, while Poisson degree distributions are quite sensitive in both cases. Then, much work has been done to extend these results. We focus here on these basic results, with the aim of deepening significantly our understanding of their origin and their limitations. We review in detail previous contributions and we give full proofs in a unified framework, in which the approximations on which these results rely are well identified. We then add to these known results a set of new ones aimed at enlightening some important aspects. We also provide extensive and rigorous experiments which make it possible to evaluate the relevance of the analytic results. We reach the conclusion that, even if it is clear that the basic results of the field are true and important, they are in practice much less striking than generally thought. The differences between random failures and attacks are not so huge and can be explained with simple facts. Likewise, the differences in the behaviors induced by power-law and Poisson distributions are not as striking as often claimed.